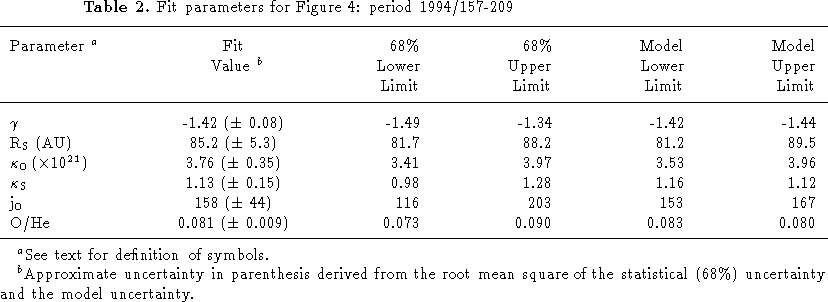
E. C. Stone and A. C. Cummings
Space Radiation Laboratory,
California Institute of Technology, Pasadena
W. R. Webber
Department of Astronomy, New Mexico State University,
Las Cruces
Using data from the Voyager and Pioneer spacecraft,
we examine the energy spectra of anomalous
cosmic rays (ACRs) during 1992 - 1994, a period
of rapidly increasing intensities of these particles in the outer heliosphere.
The 1992 period appears to be in non-equilibrium,
marked by a rapid decrease in the tilt of the current sheet
from ~ 63 to ~ 35
and a complex, evolving magnetic topology
that affects interplanetary drifts and drift acceleration along the
solar wind termination shock.
In addition, large propagating interplanetary disturbances in 1991 may
have weakened the shock
temporarily, reducing
the intensity of accelerated ions.
The 1993-1994 period appears to be in quasi-equilibrium,
marked
by a stable tilt of the current sheet and
a steady large scale magnetic topology that provides
stable conditions for propagation and acceleration.
The ACR intensities of higher rigidity particles rise slowly
during this period, suggesting that the shock intensity
has stabilized.
At lower rigidities, the ACR intensities are increasing rapidly,
which we attribute to decreasing modulation.
During 1994 days 157 - 209, we estimate that the shock was at
85 ![]() 5 AU.
The shock strength, s, is estimated to be 2.63
5 AU.
The shock strength, s, is estimated to be 2.63 ![]() 0.14, significantly weaker than a strong shock (s = 4) and consistent with a termination shock modified by the pressure of galactic cosmic rays.
By comparing these 1994 observations with those made in 1987
we estimate that the latitudinal gradient of ACR He with
energies 31 - 57 MeV/nuc is ~ 1.9%/deg along the shock from
the equator to the pole.
We estimate that the ratio of the efficiency of injection of
0.14, significantly weaker than a strong shock (s = 4) and consistent with a termination shock modified by the pressure of galactic cosmic rays.
By comparing these 1994 observations with those made in 1987
we estimate that the latitudinal gradient of ACR He with
energies 31 - 57 MeV/nuc is ~ 1.9%/deg along the shock from
the equator to the pole.
We estimate that the ratio of the efficiency of injection of
![]() to
to ![]() pickup ions into the
acceleration process is 7.0
pickup ions into the
acceleration process is 7.0 ![]() 1.6.
1.6.
Anomalous cosmic rays (ACRs) are thought to be interstellar neutrals
[Fisk et al., 1974] that have become ionized
in the interplanetary medium and accelerated in the outer heliosphere, probably
at the solar wind termination shock [Pesses et al.,
1981].
Seven elements have been identified in the ACR component: H, He, C, N, O,
Ne, and Ar
[McDonald et al., 1974; Garcia-Munoz et al., 1973;
Hovestadt et al., 1973; Cummings and Stone, 1988, 1990;
Christian et al., 1988, 1995;
McDonald et al., 1995].
Recently, observations have confirmed that the ACRs are singly-ionized
[Adams et al., 1991; Singh et al., 1991; Klecker et al., 1995],
and a study of their
gradients has suggested that the solar
wind termination shock was at 67 ![]() 5 AU in 1987
during the last period of minimum solar
activity [Cummings et al., 1994].
5 AU in 1987
during the last period of minimum solar
activity [Cummings et al., 1994].
Other recent estimates of the location of the termination shock based
on dynamic pressure balance
[Belcher et al., 1993; Whang and Burlaga, 1993;
Lallement et al., 1993],
hydrogen Lyman ![]() resonant scattering
[Hall et al., 1993], and
kilohertz radio emissions
[Grzedielski and Lazarus, 1993;
Zank et al., 1994] range from 60 to 105 AU.
However, Gurnett et al. [1993] ascribe the radio emissions to the
heliopause region located at 116 to 177 AU.
resonant scattering
[Hall et al., 1993], and
kilohertz radio emissions
[Grzedielski and Lazarus, 1993;
Zank et al., 1994] range from 60 to 105 AU.
However, Gurnett et al. [1993] ascribe the radio emissions to the
heliopause region located at 116 to 177 AU.
Cummings et al. [1994] based their estimate of the location of the termination shock in 1987 on a model in which positive particles were drifting into the inner heliosphere along the Sun's neutral sheet. The radial gradient of the ACRs was observed to be correlated with the tilt of the neutral sheet for tilts less than ~ 30. The estimate of 67 AU for the shock location was derived by using the observed tilt of the sheet to infer the local gradient of the particles and then extrapolating the ACR intensity outward from the position of the Voyager 2 (V2) and Pioneer 10 (P10) spacecraft to a location where the extrapolated intensity was steady with time.
During the current segment of the solar cycle, after the solar magnetic field reversed in 1990, the ACR particles are expected to drift downward onto the heliographic equator from the polar regions [Jokipii et al., 1977]. The cosmic ray intensity is expected to be less responsive to the changes in the tilt angle than in the A < 0 period [Le Roux and Potgieter, 1990], and hence we do not use the same technique of extrapolation to the shock that was employed for the 1987 data.
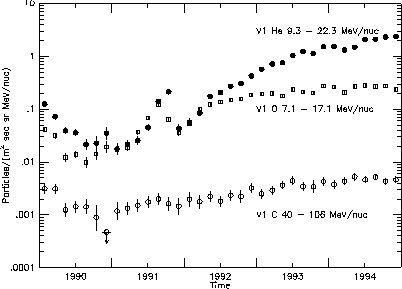
Figure 1: Intensities of cosmic rays measured at Voyager 1.
Solid
circles represent helium with 9.3 to 22.3 MeV/nucleon (0.53
to 0.82 GV); open
squares are oxygen with 7.1 to 17.1 MeV/nucleon (1.84
to 2.87 GV); and open circles
are carbon with 40 to 106 MeV/nucleon (0.55 to 0.91 GV).
In the current study we have used another technique, similar to that used by Ip [1990] for estimating the location of the solar wind termination shock, that is valid for ~ 1993 onward during periods without large transient disturbances such as Global Merged Interaction Regions (GMIRs). To estimate the location of the solar wind termination shock we employ a spherically-symmetric model of solar modulation. Preliminary accounts of this work have been presented at the 24th International Cosmic Ray Conference [Stone et al., 1995a; Stone et al., 1995b].
In Figure 1 we show the time histories of the intensity of He, O, and C observed with the cosmic-ray experiment on Voyager 1 (V1) [Stone et al., 1977]. The carbon intensity is for the energy range 40 - 106 MeV/nucleon and is entirely due to galactic cosmic rays which are fully ionized. Prior to 1992, the He intensity is a mixture of solar, galactic, and anomalous cosmic rays. By 1992, the anomalous cosmic rays dominate this intensity. The O intensity is dominated by anomalous cosmic rays throughout the period shown in Figure 1.
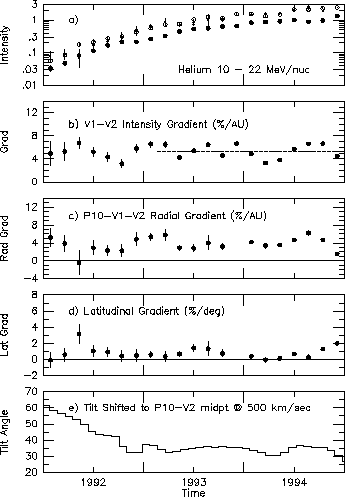
Figure 2: a) Intensity of helium (52-day averages) measured
at P10 (crosses), V2 (solid circles), and V1 (open circles) versus time.
b) Intensity gradient between V1 and V2 for He
with 9.3 - 22.3 MeV/nuc. The dashed line is the mean
for the period indicated.
c) Radial gradient of ACR He with ~ 10 - 22 MeV/nuc.
d) Latitudinal gradient of ACR He with ~ 10 - 22 MeV/nuc.
e) Estimated tilt of the neutral
current sheet shifted to the mid-point of V2 and P10.
Each tilt observation
[Hoeksema, private communication, 1994]
covers a single solar rotation or ~ 26 days.
We have performed a 3-solar-rotation moving average on the
supplied tilt data set before plotting, in order to approximate the
average conditions between V2 and P10 which are ~ 17 AU apart.
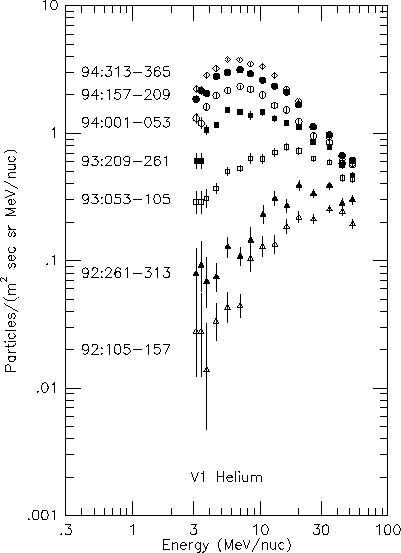
Figure 3: Energy spectrum of helium
measured at V1 for seven time periods.
The V1 He and O intensity profiles show the result of intense solar activity in early 1991. The ACR intensities rise rapidly after the effects of the transient decrease have passed. From the beginning of 1992 to the end of 1994, the ACR He intensity shows a ~ 40-fold increase and the ACR O intensity increases by a factor of ~ 3. Most of the O increase occurs during 1992, whereas the He intensity continues to increase steadily to the end of 1994. Following a small transient decrease in late 1991, the galactic cosmic ray C intensity rises by a factor of ~ 2.5 from the beginning of 1992 to the end of 1994. The energy interval of the O intensity measurements corresponds to a mean rigidity of ~ 2.4 GV, whereas the He intensity measurements correspond to a lower rigidity, ~ 0.7 GV. The equally rapid increases of the 0.7 GV and the 2.4 GV intensities in 1992 suggest a period of non-equilibrium recovery following the transient in late 1991. The much smaller increase in the 2.4 GV intensity during 1993 and 1994 suggests a period of quasi-equilibrium, during which the high-rigidity intensity is nearly the same as the unmodulated shock intensity and the lower-rigidity intensity continues to increase in response to decreasing modulation.
In Figure 2 we show the time dependence of several
parameters of interest to this study.
Figure 2c shows the
radial gradient of the 10 - 22 MeV/nuc He intensities using the
3-spacecraft method.
In this method, we assume a constant radial
and latitudinal gradient in each 52-day period and solve for each
from the two measured intensity ratios ![]() and
and
![]() ,
where
,
where ![]() ,
, ![]() , and
, and ![]() are
the intensities at P10, V2, and V1, respectively
(see Cummings et al. [1987] for more explanation).
The radial gradient
in Figure 2c shows no systematic trend
but does exhibit non-statistical variations.
are
the intensities at P10, V2, and V1, respectively
(see Cummings et al. [1987] for more explanation).
The radial gradient
in Figure 2c shows no systematic trend
but does exhibit non-statistical variations.
In Figure 2e we show the tilt of the neutral sheet [Hoeksema, 1992] shifted to the midway position between V2 and P10. The tilt is in a rapid, steady decline until approximately the beginning of 1993, at which time it levels off at ~ 35. The rapidly changing tilt in 1992 implies that the magnetic field topology in the heliosphere is also evolving in a complex way, since the Sun's magnetic field is embedded in the solar wind and carried with it into the outer heliosphere. This changing magnetic field topology will affect the drift motion of the particles as well as affecting the drift acceleration of the ACR particles at the solar wind termination shock. In addition, we might expect the GMIR [McDonald et al., 1994] that evolved from the 1991 solar activity to cause other complex changes in the magnetic field topology and in the acceleration conditions at the shock [Zank et al., 1994]. An interaction of this structure with the heliopause is thought to be responsible for the low-frequency radio emissions observed in 1992 and 1993 by the plasma wave experiment on the Voyager spacecraft [Gurnett et al., 1993].
In Figure 3 we show the energy spectrum of He at V1 for seven 52-day periods beginning with 1992/105 - 157 and ending with 1994/313 - 365. For the two 1992 spectra, the entire energy spectrum is growing in intensity uniformly over the full energy range shown ( ~ 3 to 60 MeV/nuc). This is consistent with a non-equilibrium period caused by effects on the drift of the particles from the changing magnetic field topology (Figure 2e) and effects of the 1991 GMIR on the strength of the termination shock. Beginning in 1993 the high-energy end of the spectrum changes intensity only slowly, whereas the lower-energy end continues to rise rapidly. This is consistent with the onset of a quasi-equilibrium period with a stable magnetic field topology (see Figure 2e) giving rise to stable conditions for acceleration and propagation. The continued increase in intensities at low energies could result from an energy-dependent mean free path that is increasing with time or a decreasing distance between the shock and V1. The intensity increase is smaller at high energies where the modulation between the shock and the spacecraft is small. We note that the energy of the peak intensity of ACR He is ~ 6 MeV/nuc in late 1994, lower than previously observed and consistent with a lower level of ACR modulation than at any time in the past.
In order to estimate the distance to the termination shock, we have compared our observations at V1 and V2 during the quasi-equilibrium period in 1993 and 1994 with a spherically-symmetric equilibrium model of the propagation of ACRs. In 1987 there were large latitudinal gradients of ACRs which would have made meaningful comparison with a spherically-symmetric model difficult. Figure 2a shows 52-day average intensities of helium observed on V1, V2, and P10 with energies ~ 10 - 22 MeV/nuc during 1992 - 1994. From the shape of the energy spectra we believe the intensity in this energy interval is dominated by ACRs throughout the period shown, although the first two periods in 1992 have substantial contributions from galactic cosmic rays (GCRs). The intensities at all 3 spacecraft increase by a factor of ~ 40 from the beginning of 1992 to the end of 1994. The P10 and V1 intensities are in approximate agreement, although P10 leads V1 by a distance which varies from 6.2 to 4.2 AU during this period, and we would expect that the P10 intensity would be somewhat larger than the intensity at V1 if spherical symmetry prevails. The intensity at V2 is consistently lower than the intensity at P10 and V1.
In Figure 2d we show the latitudinal gradients, which show no systematic trend and the mean is 0.78 %/deg or equivalently ~ 0.8%/AU in the latitudinal direction as compared with ~ 4%/AU in the radial direction (see Figure 2c). Although the intensity gradient is mainly radial and therefore resembles that of a spherically-symmetric model, the small positive latitudinal gradient means that the spectrum observed out of the heliographic equatorial plane at a given radius corresponds to that which would be observed at a somewhat larger ``effective radius'' in the equatorial plane. We use the following equation to estimate the effective location of a particular spacecraft:
![]()
where
![]() is the average latitudinal gradient and
is the average latitudinal gradient and ![]() is the effective location,
is the effective location, ![]() is the actual location,
and
is the actual location,
and
![]() is the latitude of the spacecraft, and
where we have used a model in which the radial gradient
in the intensity j is proportional
to 1/r, with
is the latitude of the spacecraft, and
where we have used a model in which the radial gradient
in the intensity j is proportional
to 1/r, with
![]() .
In this work we assume the particle distributions
are symmetrical about the heliographic equator [Jokipii, 1990], so
we use the absolute value of the spacecraft latitude in all cases.
.
In this work we assume the particle distributions
are symmetrical about the heliographic equator [Jokipii, 1990], so
we use the absolute value of the spacecraft latitude in all cases.
We thus need to know the average latitudinal gradient ![]() and the average radial gradient parameter
and the average radial gradient parameter ![]() .
.
![]() is related to the
3-spacecraft radial gradient,
is related to the
3-spacecraft radial gradient, ![]() ,
by
,
by
![]()
where ![]() and
and ![]() are the radial positions of P10 and V2,
respectively, and
are the radial positions of P10 and V2,
respectively, and ![]() is the
radial separation distance
between them.
is the
radial separation distance
between them.
It is important to pick time periods for study in which transient disturbances at V1 and V2 are absent. In Figure 2b we show the gradient of the intensities from V1 to V2:
![]()
where ![]() is the difference
in the radial distances of V1 and V2.
This gradient is clearly affected by transient disturbances
but appears to show no systematic decrease or increase
from 1992 through 1994.
Although the latitudinal gradient (0.8%/deg,
is the difference
in the radial distances of V1 and V2.
This gradient is clearly affected by transient disturbances
but appears to show no systematic decrease or increase
from 1992 through 1994.
Although the latitudinal gradient (0.8%/deg, ![]() ~
~ ![]() )
contributes, this intensity gradient is dominated
by the radial gradient ( ~ 4%/AU,
)
contributes, this intensity gradient is dominated
by the radial gradient ( ~ 4%/AU, ![]() ~ 12 AU).
The near constancy
of the intensity gradient implies that
~ 12 AU).
The near constancy
of the intensity gradient implies that ![]() ,
where
,
where ![]() is the Compton-Getting factor (equal to [2 - 2
is the Compton-Getting factor (equal to [2 - 2 ![]() ]/3 for
non-relativistic particles, where
]/3 for
non-relativistic particles, where
![]() is the average power-law index of the differential
energy spectrum),
V is the solar wind velocity, and
is the average power-law index of the differential
energy spectrum),
V is the solar wind velocity, and ![]() is the
radial diffusion coefficient, is approximately
unchanged while the intensities are increasing by a
factor of ~ 40.
From Figure 2b, we pick two recent 52-day periods,
1994/157-209 and 1993/157-209, which have V1/V2 intensity
gradients near the mean value.
is the
radial diffusion coefficient, is approximately
unchanged while the intensities are increasing by a
factor of ~ 40.
From Figure 2b, we pick two recent 52-day periods,
1994/157-209 and 1993/157-209, which have V1/V2 intensity
gradients near the mean value.
For this study, we use the radial and latitudinal gradients
from 1993/52 - 1994/365, representing twelve 52-day periods in Figures
2c and 2d, in computing the parameters
involved in calculating the effective radial locations
for the V1 and V2 spacecraft.
The average radial gradient, latitudinal gradient,
and radial gradient parameter for the twelve
periods are ![]() %/AU,
%/AU,
![]() %/deg,
and
%/deg,
and ![]() .
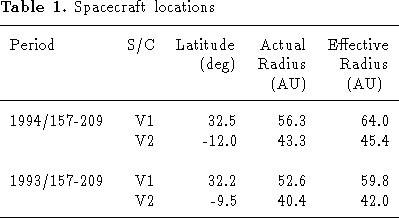
In Table 1 we show the actual radius and latitude for V1
and V2 for the two selected time periods along with the
calculated effective radial positions used in the model fits.
.
In Table 1 we show the actual radius and latitude for V1
and V2 for the two selected time periods along with the
calculated effective radial positions used in the model fits.
In the model calculations
we fit both the ACR helium and oxygen spectra at V1 and V2.
The ACR He
shock spectrum is assumed to be a power-law in energy per nucleon,
![]() .
The ACR O shock spectrum is assumed to
be a power-law with the same index.
For O this is an adequate approximation for energies up to ~ 10 MeV/nuc.
Above ~ 10 MeV/nuc we will later show that the energy spectrum exhibits
an approximately exponential roll-off.
Similarly, for ACR He this approximation is valid up
to ~ 60 MeV/nuc.
We assume the diffusion coefficient,
.
The ACR O shock spectrum is assumed to
be a power-law with the same index.
For O this is an adequate approximation for energies up to ~ 10 MeV/nuc.
Above ~ 10 MeV/nuc we will later show that the energy spectrum exhibits
an approximately exponential roll-off.
Similarly, for ACR He this approximation is valid up
to ~ 60 MeV/nuc.
We assume the diffusion coefficient,
![]() (in
(in ![]() ), is
given by
), is
given by
![]()
where ![]() is a scaling factor,
is a scaling factor, ![]() is particle speed,
r is heliocentric radial distance in AU, and R is rigidity in GV.
This form for the radial and rigidity dependence of
is particle speed,
r is heliocentric radial distance in AU, and R is rigidity in GV.
This form for the radial and rigidity dependence of ![]() can be derived from the quasilinear formulation of
Bieber et al. [1995] in which
can be derived from the quasilinear formulation of
Bieber et al. [1995] in which
![]() ,
where
,
where ![]() is the Larmour radius (
is the Larmour radius ( ![]() ),
),
![]() the gyrofrequency,
the gyrofrequency,
![]() the scattering time, and
the scattering time, and
![]() .
Following Bieber et al., we assume that the coherence length
of the magnetic field scales as r (
.
Following Bieber et al., we assume that the coherence length
of the magnetic field scales as r ( ![]() ), that
the root mean square field fluctuations are proportional to the mean field
(
), that
the root mean square field fluctuations are proportional to the mean field
( ![]() ), and that
), and that
![]() for
for ![]() 1 AU.
1 AU.
There are six free parameters in the model:
the shock location ( ![]() ), the diffusion
coefficient scaling factor (
), the diffusion
coefficient scaling factor ( ![]() ),
the diffusion coefficient shape factor (
),
the diffusion coefficient shape factor ( ![]() ),
the power-law index (
),
the power-law index ( ![]() ) of the energy
spectrum at the shock, the intensity scaling factor (
) of the energy
spectrum at the shock, the intensity scaling factor ( ![]() )
of the
ACR He shock spectrum, and the ratio of O to He at the shock (O/He).
We assume the solar wind velocity, V, is constant at 500
)
of the
ACR He shock spectrum, and the ratio of O to He at the shock (O/He).
We assume the solar wind velocity, V, is constant at 500 ![]() ,
which is close to the average value at V2 of 490
,
which is close to the average value at V2 of 490 ![]() for 1993/1 - 1994/365 [Richardson, private communication, 1995].
The fits are sensitive to
for 1993/1 - 1994/365 [Richardson, private communication, 1995].
The fits are sensitive to ![]() and V only in the ratio
and V only in the ratio ![]() .
.
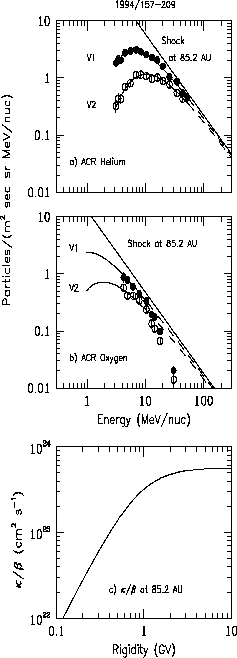
Figure 4: a) Energy spectra of ACR helium at the positions of V1 and V2
spacecraft for the period 1994/157-209.
The curves represent the 6-parameter best-fit energy spectra at the
solar wind termination shock, V1, and V2, as described in the text.
b) Same as a) except for ACR oxygen.
c) Best-fit diffusion coefficient divided by particle velocity
versus rigidity. The form of the diffusion coefficient
is described in the text.
The data and best-fit model curves for the period
1994/157 - 209 are shown in Figures 4a and 4b.
The fits were made only in the energy regions shown
by the solid lines.
The ![]() of the six-parameter best fit to
the 39 data points in Figure 4 is 13.3.
Figure 4c shows the best-fit diffusion coefficient as
a function of rigidity.
of the six-parameter best fit to
the 39 data points in Figure 4 is 13.3.
Figure 4c shows the best-fit diffusion coefficient as
a function of rigidity.
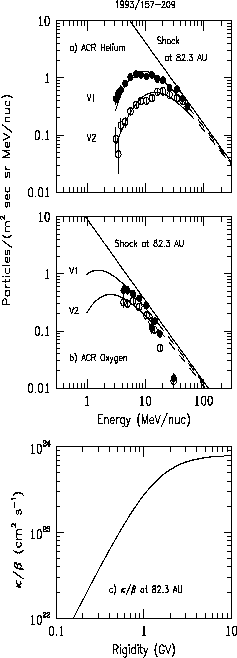
Figure 5: Same as Figure 4 except the
period is 1993/157-209 and the shock
power-law spectral index is fixed at -1.42
and the O/He ratio is fixed at 0.081.
We investigated the confidence limits for each parameter in
two ways. We first estimated the 68% confidence limits
by iteratively changing and fixing the value of one parameter
and re-fitting until we found the parameter value where the ![]() had increased by 1 (see Press et al. [1992]).
We did this in turn for all six parameters.
The best-fit parameter values and the
68% confidence limits are shown in
Table 2 for the period 1994/157-209.
had increased by 1 (see Press et al. [1992]).
We did this in turn for all six parameters.
The best-fit parameter values and the
68% confidence limits are shown in
Table 2 for the period 1994/157-209.
In the second method we account
for modelling uncertainties
by estimating the uncertainty in the effective radial
positions of V1 and V2 using equation 1
together with the uncertainties in the parameters
![]() and
and ![]() .
We find that the uncertainties on the effective radial
positions were 2 AU for V1 and 0.5 AU for V2.
We performed two fits, one using the upper limits for the
effective radial locations for V1 and V2
and another using the lower limits.
The resulting parameters are
shown as the model limits in Table 2.
.
We find that the uncertainties on the effective radial
positions were 2 AU for V1 and 0.5 AU for V2.
We performed two fits, one using the upper limits for the
effective radial locations for V1 and V2
and another using the lower limits.
The resulting parameters are
shown as the model limits in Table 2.
The shock strength (see, e.g., Potgieter and Moraal [1988]),
s, is related to the spectral index by:
![]() .
From the values of
.
From the values of ![]() in Table 2, the inferred strength
of the shock
is 2.63
in Table 2, the inferred strength
of the shock
is 2.63 ![]() 0.14.
The shock is therefore not a strong shock (s = 4;
0.14.
The shock is therefore not a strong shock (s = 4; ![]() = -1)
and it may be modified by cosmic rays
(see, e.g., Donohue and Zank [1993]).
We estimate that the shock location is ~
= -1)
and it may be modified by cosmic rays
(see, e.g., Donohue and Zank [1993]).
We estimate that the shock location is ~ ![]() AU
during the period 1994/157-209 (see Table 2).
AU
during the period 1994/157-209 (see Table 2).
In Figure 5 we show the ACR He and O spectra at V1 and V2
for the period 1993/157 - 209 along with a
4-parameter model fit ( ![]() = 1.1).
We held the shock spectral index fixed at -1.42 and
the shock
O/He ratio fixed at 0.081,
the values from the 1994 period.
The fit indicates that the shock distance has not changed
appreciably over the year
despite the fact that the peak intensity at V1 has
increased by a factor of ~ 3.
The best-fit parameters and limits are shown in Table 3.
This intensity increase is apparently due to
a combination of two effects (see Tables 2 and 3):
1) the ratio of the diffusion coefficient
at the peak energy of the He spectrum to solar wind
velocity has increased by ~ 50% and 2) the best-fit shock
intensity scaling parameter increased by ~ 40%,
much less than the factor of ~ 3 increase in the V1 peak intensity.
The relatively constant shock intensity is
consistent with quasi-equilibrium conditions
for shock acceleration.
During the two year period around the last solar minimum,
Cummings et al. [1994] also found that a constant
shock intensity was consistent with observed ACR He and O
intensities that changed by factors of ~ 5 and ~ 8, respectively.
= 1.1).
We held the shock spectral index fixed at -1.42 and
the shock
O/He ratio fixed at 0.081,
the values from the 1994 period.
The fit indicates that the shock distance has not changed
appreciably over the year
despite the fact that the peak intensity at V1 has
increased by a factor of ~ 3.
The best-fit parameters and limits are shown in Table 3.
This intensity increase is apparently due to
a combination of two effects (see Tables 2 and 3):
1) the ratio of the diffusion coefficient
at the peak energy of the He spectrum to solar wind
velocity has increased by ~ 50% and 2) the best-fit shock
intensity scaling parameter increased by ~ 40%,
much less than the factor of ~ 3 increase in the V1 peak intensity.
The relatively constant shock intensity is
consistent with quasi-equilibrium conditions
for shock acceleration.
During the two year period around the last solar minimum,
Cummings et al. [1994] also found that a constant
shock intensity was consistent with observed ACR He and O
intensities that changed by factors of ~ 5 and ~ 8, respectively.
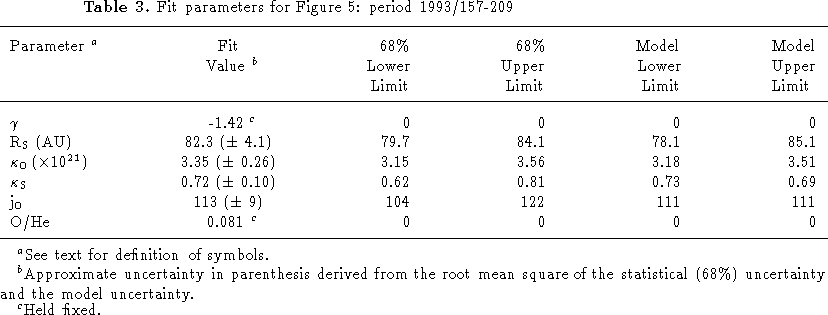
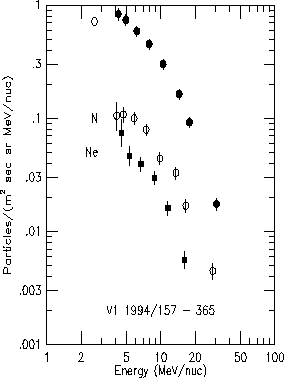
Figure 6: Energy spectra of ACR O, N, and Ne for the period
1994/157 - 365.
Small (< 10%) corrections for GCRs have
been made before plotting.
In Figures 4b and 5b the observed ACR
oxygen spectra exhibit a roll-off in intensity
above ~ 10-15 MeV/nuc.
This roll-off is present in other spectra as well as shown
in Figure 6 where the
V1 ACR O, N, and Ne spectra are displayed
for the period
1994/157 - 365.
Note that all 3 spectra show the roll-off in intensity above
~ 10-15 MeV/nuc.
This roll-off in the energy spectra
is consistent with that expected in diffusive shock acceleration
if the shock has a finite radius of curvature.
Such a roll-off is predicted to occur when ![]() is
of order unity (see, e.g, Potgieter and Moraal [1988]),
where V is the solar wind velocity,
is
of order unity (see, e.g, Potgieter and Moraal [1988]),
where V is the solar wind velocity, ![]() is the diffusion coefficient
in the vicinity of the shock, and
is the diffusion coefficient
in the vicinity of the shock, and ![]() is the shock radius.
is the shock radius.
Another interpretation of the roll-off in the energy spectrum is due to Jokipii [1990]. In his theory the ACR particles gain their energy by drifting along the shock from the equator to the pole during the A > 0 portion of the solar cycle (pole to equator during A < 0). The maximum energy gain is set by the electrostatic potential difference between the heliospheric equator and pole and is ~ 240 MeV. Since the ACR particles are singly ionized, the energy spectra of the different ACR ions would be expected to roll-off above ~ 240 MeV.
In Figure 7 we plot the V1 differential energy spectra of ACR H, He, N, O, and Ne for the period 1994/157-365 as a function of energy instead of energy/nucleon. The intensities have been normalized before plotting by the factors shown in the figure. At low energies, the effect of solar modulation causes the H and He spectra to peak at different energies. However, the agreement of the different spectra is good near the break which occurs at ~ 170 - 240 MeV, in rough agreement with the shock-drift limit of Jokipii [1990]. We do not feel that we can distinguish experimentally between the two possible interpretations of the roll-off in the shock spectra.
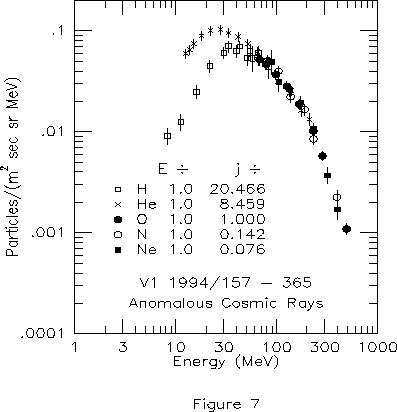
Figure 7: Composite V1 energy spectrum of O
for the period 1994/157-365 plotted as a function
of total energy.
The energy spectra of the different individual ions
are normalized to O by the factors shown in the figure.
The shock spectra of ACR He and O in Figures 4a and 4b are
the spectra expected
at the shock in the heliographic equator for the period
1994/157-209.
Likewise, the shock spectra derived by Cummings et al. [1994]
for the period 1987/105-313 are the spectra expected
at the shock in the heliographic equator.
For the 1987 period the intensity of ACR He at the shock
in the energy range 31 - 57 MeV/nuc
was determined to be 4.3 ![]() .
From Figure 4a the ACR He shock intensity during 1994/157-209
in this same energy range is
0.77
.
From Figure 4a the ACR He shock intensity during 1994/157-209
in this same energy range is
0.77 ![]() .
Thus the intensity at the shock
at the heliographic
equator in 1994 is a factor of ~ 5.5 smaller than it was
in 1987.
This difference can be understood in the context of
shock-drift acceleration [Jokipii, 1990] that causes
the intensity to vary along the shock from the equator to
the pole, the intensity being a maximum at the pole during the 1994 period (A > 0)
and a maximum at the equator during 1987 (A < 0).
Interpreted in this way the factor of 5.5 difference observed in
the 1994 shock intensity compared to the 1987 shock intensity could correspond to the
latitudinal difference in the intensity at the equator and the pole in either of the years 1994
or 1987.
This would imply a latitudinal gradient
along the shock of 1.9%/deg from the equator to the pole
during 1994/157-209, in qualitative agreement with shock drift acceleration.
In Table 4 we show this value of the latitudinal gradient along with
several other recent determinations
for the latitudinal gradient of ACRs, most of which are based on comparisons
of Ulysses measurements at high latitude with measurements near the ecliptic plane.
In general there is a correspondence of these measurements with the
implied latitudinal gradient along the shock.
.
Thus the intensity at the shock
at the heliographic
equator in 1994 is a factor of ~ 5.5 smaller than it was
in 1987.
This difference can be understood in the context of
shock-drift acceleration [Jokipii, 1990] that causes
the intensity to vary along the shock from the equator to
the pole, the intensity being a maximum at the pole during the 1994 period (A > 0)
and a maximum at the equator during 1987 (A < 0).
Interpreted in this way the factor of 5.5 difference observed in
the 1994 shock intensity compared to the 1987 shock intensity could correspond to the
latitudinal difference in the intensity at the equator and the pole in either of the years 1994
or 1987.
This would imply a latitudinal gradient
along the shock of 1.9%/deg from the equator to the pole
during 1994/157-209, in qualitative agreement with shock drift acceleration.
In Table 4 we show this value of the latitudinal gradient along with
several other recent determinations
for the latitudinal gradient of ACRs, most of which are based on comparisons
of Ulysses measurements at high latitude with measurements near the ecliptic plane.
In general there is a correspondence of these measurements with the
implied latitudinal gradient along the shock.

The energy density of the ACR He shock spectrum
in Figure 4a
above an injection velocity of 2 ![]() (5.2 keV/nuc for
(5.2 keV/nuc for ![]() is ~ 0.005 eV/
is ~ 0.005 eV/ ![]() .
The corresponding value for ACR O in Figure 4b is
~ 0.001 eV/
.
The corresponding value for ACR O in Figure 4b is
~ 0.001 eV/ ![]() .
We can estimate the ACR H shock spectrum by scaling from
the ACR He shock spectrum.
Cummings et al. [1984] found that the ACR energy
spectra of the different elements scale to
each other with linear factors
in energy and intensity if the
diffusion coefficient is proportional to
.
We can estimate the ACR H shock spectrum by scaling from
the ACR He shock spectrum.
Cummings et al. [1984] found that the ACR energy
spectra of the different elements scale to
each other with linear factors
in energy and intensity if the
diffusion coefficient is proportional to ![]() .
The peak energies of the ACR H and He spectra
are in the rigidity range ( ~ 0.3-0.4 GV)
where
.
The peak energies of the ACR H and He spectra
are in the rigidity range ( ~ 0.3-0.4 GV)
where ![]() is ~ 2 (see Figures 4c and 5c).
This implies an energy scaling factor of 6.3
(see Cummings et al., [1984]).
The intensity scaling factor is 0.40
is ~ 2 (see Figures 4c and 5c).
This implies an energy scaling factor of 6.3
(see Cummings et al., [1984]).
The intensity scaling factor is 0.40 ![]() 0.02 from
Cummings and Stone [1995] for a period only
slightly different from the one shown in Figure 4.
Using these factors and the He spectrum from
Figure 4a we estimate that the power-law portion
of the ACR H shock spectrum
for the period 1994/157-209 is given by
0.02 from
Cummings and Stone [1995] for a period only
slightly different from the one shown in Figure 4.
Using these factors and the He spectrum from
Figure 4a we estimate that the power-law portion
of the ACR H shock spectrum
for the period 1994/157-209 is given by
![]() .
This implies an energy density of ACR H at the shock of 0.009
eV/
.
This implies an energy density of ACR H at the shock of 0.009
eV/ ![]() ,
yielding a total ACR
energy density of 0.015
,
yielding a total ACR
energy density of 0.015 ![]() 0.002 eV/
0.002 eV/ ![]() .
The estimated uncertainty includes uncertainty in
.
The estimated uncertainty includes uncertainty in ![]() from
Table 2 and the uncertainty in scaling the He shock spectrum to the
H shock spectrum.
For comparison, the energy density of the solar wind
at low heliographic latitudes at 85 AU is ~ 1.2 eV/
from
Table 2 and the uncertainty in scaling the He shock spectrum to the
H shock spectrum.
For comparison, the energy density of the solar wind
at low heliographic latitudes at 85 AU is ~ 1.2 eV/ ![]() , as scaled
from ~ 16 eV/
, as scaled
from ~ 16 eV/ ![]() at 23 AU
(derived from Figure 1 of Grzedielski and Lazarus [1993]).
Thus the ACR energy density is only ~ 1% that of the solar wind.
at 23 AU
(derived from Figure 1 of Grzedielski and Lazarus [1993]).
Thus the ACR energy density is only ~ 1% that of the solar wind.
This ACR energy density is similar to that derived for the 1987 period by Cummings et al. [1994]. However, Cummings et al. [1994] assumed a strong shock with a power-law index at low energies of -1. The modulation effects were stronger in the 1987 spectrum at ~ 23 AU than they are in the 1994 spectrum at ~ 56 AU, and the peak energy of the 1987 ACR He spectrum was ~ 20-25 MeV/nuc compared to ~ 6 MeV/nuc at V1 in 1994 (see Figure 4a). Consequently, in the 1987 observation there was very little information on the power-law index of the shock spectrum. In Figure 8 we reproduce Figure 5b from Cummings et al. [1994] with the addition of lines indicating possible shock spectra with power-law index = -1.42 in 1987. Assuming this index was -1.42 in 1987 results in somewhat higher estimates of the energy density of ACRs at the shock than were derived in Cummings et al. [1994]. In Table 5 we show the estimated energy density for the 1994 period along with the old and new estimates for 1987. We also compare to the estimated energy density of the solar wind at the location of the shock. If we assume that the 1987 measurements with index -1.42 correspond to the maximum ACR intensity at the shock, then the energy density of ACRs is ~ 5% of the solar wind energy density in the region with maximum source intensity in 1994.
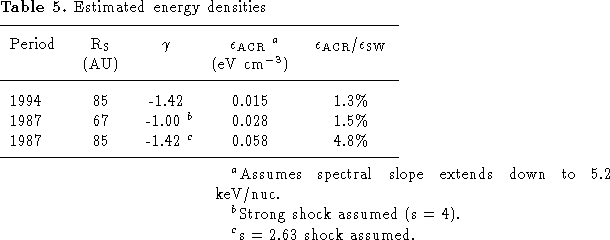
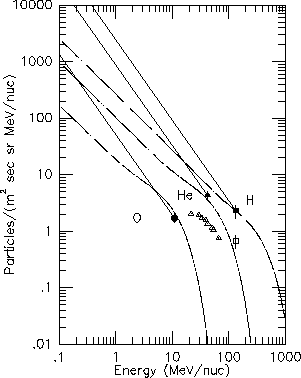
Figure 8: Same as Figure 5b from Cummings et al. [1994]
showing the energy spectra of ACR O, He, and H
for the period 1987/105-313.
The open points are observations from V2.
The solid points are the deduced
intensities at the termination shock.
Three power-law lines have been added, normalized
to the shock intensities, with power-law index -1.42
to indicate a possibly more realistic energy dependence of the
shock spectra.
To estimate the efficiency ![]() for the injection of pickup ions into
the acceleration process, we follow the calculations of
Lee [1983] from which it can be shown
that the accelerated spectrum is given in units of
for the injection of pickup ions into
the acceleration process, we follow the calculations of
Lee [1983] from which it can be shown
that the accelerated spectrum is given in units of
![]() by
by
![]()
where ![]() for a downstream/upstream density ratio of 2.63,
for a downstream/upstream density ratio of 2.63,
![]() is the pickup ion flux
at the shock, and
is the pickup ion flux
at the shock, and ![]() is the injection energy
corresponding to 2
is the injection energy
corresponding to 2 ![]() ,
taken here to be
,
taken here to be ![]() MeV/nuc.
The pickup ion fluxes at the shock can be estimated
from the observations of
Gloeckler et al. [1993], who inferred the density
of neutral H and He in the outer heliosphere
as 0.077
MeV/nuc.
The pickup ion fluxes at the shock can be estimated
from the observations of
Gloeckler et al. [1993], who inferred the density
of neutral H and He in the outer heliosphere
as 0.077 ![]() 0.015 and 0.013
0.015 and 0.013 ![]() 0.003
0.003 ![]() , respectively.
Using these values, the model of Vasyliunas and Siscoe [1976]
for the distribution of these neutrals throughout the
heliosphere, and the long-term ionization rates at 1 AU of
, respectively.
Using these values, the model of Vasyliunas and Siscoe [1976]
for the distribution of these neutrals throughout the
heliosphere, and the long-term ionization rates at 1 AU of
![]() for H and
for H and
![]() for He
[Gloeckler et al., 1993],
we estimate that the fluxes of H and He pickup ions at the nose
of the heliosphere at 85 AU are
8500
for He
[Gloeckler et al., 1993],
we estimate that the fluxes of H and He pickup ions at the nose
of the heliosphere at 85 AU are
8500 ![]() 1700
1700 ![]() and
220
and
220 ![]() 50
50 ![]() , respectively.
, respectively.
Using these pickup ion fluxes, the calculated ACR He spectrum
from Lee [1983] of
![]()
![]() can be compared with the observed
can be compared with the observed
![]()
![]() to yield
to yield ![]() .
The estimated uncertainty includes the uncertainty in
.
The estimated uncertainty includes the uncertainty in ![]() from Table 2 and the uncertainty in the pickup ion flux,
from Table 2 and the uncertainty in the pickup ion flux, ![]() .
For H the calculated spectrum is
.
For H the calculated spectrum is ![]()
![]() and the ``observed''
spectrum is
and the ``observed''
spectrum is ![]()
![]() We thus find that the injection efficiency for H is
We thus find that the injection efficiency for H is
![]() ,
where we include an additional uncertainty due to
the scaling of the He shock spectrum to the H shock spectrum.
The ratio of the injection efficiencies of
,
where we include an additional uncertainty due to
the scaling of the He shock spectrum to the H shock spectrum.
The ratio of the injection efficiencies of ![]() and
and ![]() is relatively better determined than the
absolute injection efficiencies of either because the spectral
index uncertainty is removed in the ratio.
We estimate that the ratio of the efficiency of injection of
is relatively better determined than the
absolute injection efficiencies of either because the spectral
index uncertainty is removed in the ratio.
We estimate that the ratio of the efficiency of injection of
![]() to
to ![]() pickup ions into the
acceleration process is 7.0
pickup ions into the
acceleration process is 7.0 ![]() 1.6,
where we have used the He to H scaling uncertainty
in the shock spectra (16%) and the uncertainty on the
ratio of the neutral densities of H to He
in the outer heliosphere from Gloeckler et al. [1993] (17%) in
estimating the uncertainty in the ratio.
The observed preferential injection for
1.6,
where we have used the He to H scaling uncertainty
in the shock spectra (16%) and the uncertainty on the
ratio of the neutral densities of H to He
in the outer heliosphere from Gloeckler et al. [1993] (17%) in
estimating the uncertainty in the ratio.
The observed preferential injection for ![]() compared
to
compared
to ![]() is qualitatively consistent with Monte Carlo
studies of shock acceleration by Ellison et al. [1981].
is qualitatively consistent with Monte Carlo
studies of shock acceleration by Ellison et al. [1981].
Our estimates of energy spectra and shock location correspond to the upwind termination shock in the heliographic equator, since both V1 and V2 are headed outward in that general direction. Even if the termination shock is elongated in the downwind direction (see, e.g., Seuss et al., [1987]) the nose region of the upwind shock should be reasonably approximated by a spherically-symmetric diffusion model. In the downwind direction, azimuthal diffusion parallel to the magnetic field will become increasingly important with increasing shock elongation, tending to reduce upwind/downwind asymmetries in the ACR intensities.
We will continue to monitor the evolution of the energy spectra of ACRs at V1 and V2 and look for further clues to the strength of the shock and its location. The energy of the peak intensity should continue to decrease as the spacecraft approaches the shock. As the modulation lessens, the convergence of the V1 and V2 spectra should continue to lower energies and we will obtain a better estimate of the shock spectrum spectral index. As solar activity increases from the solar minimum conditions in 1998, the shock may move rapidly inward (see, e.g., Whang and Burlaga [1993]) from its position at ~ 85 AU and perhaps overrun the positions of the V1 and P10 spacecraft, which will both be at ~ 72 AU, some 5 AU beyond the estimated location of the shock 11 years earlier [Cummings et al., 1994].
We are grateful to J. T. Hoeksema for providing the tilt observations prior to publication. We thank J. Richardson and J. Belcher for providing the Voyager 2 solar wind speed data. This work was supported by NASA under contract NAS7-918.

The Distance to the Solar Wind Termination Shock in 1993 and 1994 from Observations of Anomalous Cosmic Rays
This document was generated using the LaTeX2HTML translator Version 96.1-d (Mar 10, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 pap_preprint.tex.
The translation was initiated by Steve Sears on Wed Mar 27 16:46:13 PST 1996